貌似有人怀疑土豆不会有机化学ovo所以还是展示一下ovo
手动狗头 正文开始
本篇亮点问题:熵和分子结构的联系;ΔG、ΔH、ΔS判断有机化学反应方向时的权重;键解离能的比较,张力的定义。
不要看本篇内容多,其实就是在讲张力能 的定义,为了讲这个概念引入了评价分子能量的热力学函数 ,再介绍了一系列分子能量测定和估算的方法,最后把按稳定分子推算出的估计值和实际值之间的差距归因到结构张力上,推出张力的概念。
因此本篇包含了很多统计热力学 和量子力学 的内容,这些东西没学过的几乎不可能看懂,学过的看了又得不到什么新知识,所以原本想直接跳过,但看到有初学者想挑战一下,就摘了下来,看看结论也好。总之,不要沉迷在物化和量化中,这些不是重点。
2.1 稳定分子的热力学
结构和能量是紧密联系在一起的。任何结构都对应着一个"总能量"或称"内能 "。
讨论化学结构的能量时,内能只有在与其他分子比较时才显得重要。
有机分子的能量可以用各种各样的实验值来表示,不同的能量与结构之间存在着明显的系统差异。
2.1.1 内部张力和相对稳定性
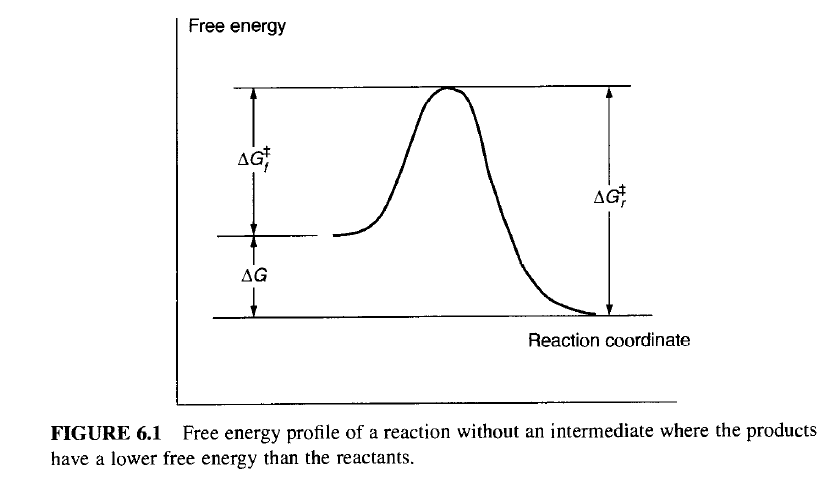
本节的要点是理解分子能量图,这种图现在的文章中经常会出现,比如下面图这种,它们多是理论计算结果。
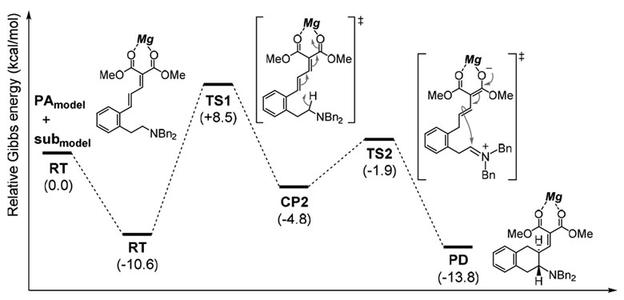
上图的纵坐标是“relative Gibbs energy”为什么是相对的呢。因为化学中讨论的张力 指存在于分子结构中的应力,而且一定是相对于参照体系而言的。
所有测得的热力学数值都是一个相对数值,必须相对于一个参考态,张力能也如此。存在张力的分子比参照体系具有更高的内能。 参照体系可以是一个不存在张力的相同分子的不同构象,或者是不存在张力的另外一个完全不同分子。
内能是分子内部包含的能量。 当有一个出路如进行化学反应时该能量可以被部分释放出来。
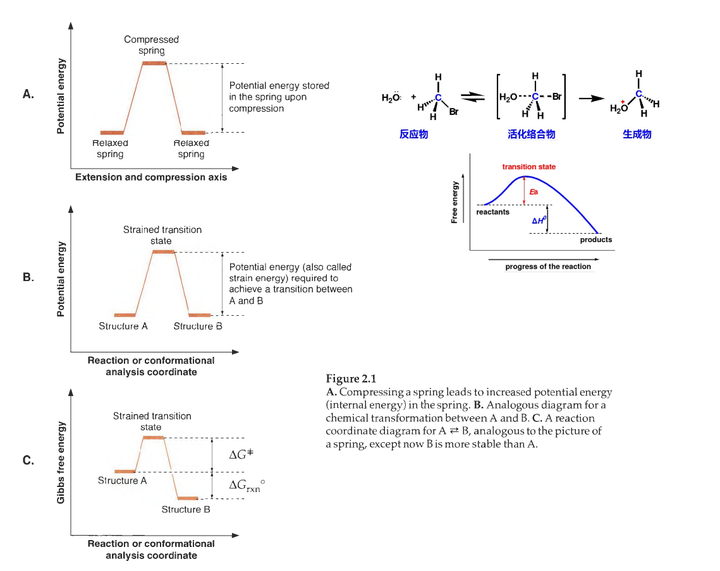
与势能类似,化学家在画反应坐标示意图和构象分析图时,常常将能量轴标记为PE或E。我们把这样的示意图称为势能图(或势能面) ,它们决定了分子内部的运动或者可能的化学反应。
它们也清楚地诠释了内能相对较高的结构可以释放出能量这种概念。不过我们也常常会采用Gibbs 自由能或焓这些更加明确的概念来定义分子的能量。
上图中弹簧的例子是为了使同学对横坐标“反应或构象分析坐标”有更好的理解,右边再给出一个Sn2反应的例子,体会一下。
分子可以占据不同的量子化能态,这些能态与分子内部的振动和电子状态密切相关。
就像弹簧一样,为了得到具有张力或者高能态的结构,必须增加分子的能量。这些能量可以通过碰撞或捕捉光子获得,也可以在化学合成过程中储存在分子内部。还有一部分能量来自溶液中的热能,它是通过温度来量度的。量子化的不同能态或是具有张力的化学结构的分布都与温度相关。
其他增加分子的能量方法例如,分子吸收红外辐射的光子可以生成具有激发振动模式的高能分子 ,或者吸收紫外线光子可以生成高能电子态。这些方法也都可以增加分子的势能。化学家通常不把这些分子的高能态与张力联系起来,然而两者之间其实是有联系的。
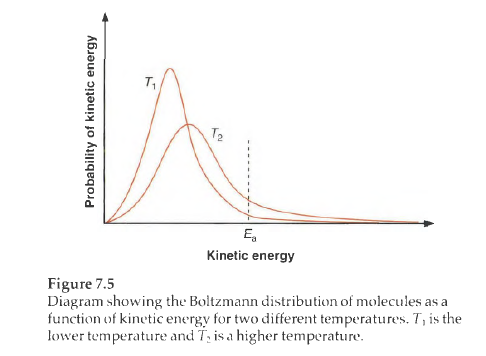
当然分子的变化肯定比弹簧复杂,能量对分子结构的影响是符合Boltzmann 分布 的。
总之,当把一个分子画在势能图上的较高位置时,它表示该分子比图中较低位置的参照分子具有更高的内能。化学家称这样的分子为高能的 、不稳定的 ,或是具有张力的 。在讨论导致张力或稳定性的因素之前,需要复习一下热力学中的一些基本概念。这样才可以更深刻地理解化学家在研究化学稳定性和张力时所使用的势能形式。
2.1.2 能量的类型
本节学过物化可以跳过,没学过的只用看结论,因为真的很无聊。
Gibbs自由能
吉布斯自由能(Gibbs free energy)是在化学热力学中为判断过程进行的方向而引入的热力学函数。
最有名的定义是G = H − TS
而它的微分形式是
dG = − SdT + Vdp + μdN,我们先讨论更本质的微分形式。
其中μ是化学势,化学势的概念比Gibbs自由能更本质,本书第三章讨论溶液时会仔细讨论化学势的问题,这里先贴一部分第三章的内容。

在以上的叙述中,实质上我们是把粒子数看作是一个参量,它对于每一个物体而言,都具有给定的常数值。现在,我们形式上把N也看作是一个自变量。于是在热力学恒等式中,应当附加一个正比子dN的项。例如,我们把能量的全微分写为: dE-TdS-PdV+μdN,
式中我们用从来表示偏微商
μ这个量称为物体的化学势。
注意以上公式中的
E =E(S,V,N)
dE = TdS - pdV +μdN
也就是说,一个体系的能量U或者说E,不考虑其他因素,可以写成E(S,V,N),也就是说它是熵S(混乱度)、V(体积)、N(粒子数)的函数,这三个都是广延变量,简单说就是可以叠加的。从微观角度上说,不考虑磁场、电场等外界因素,体系的能量是粒子的数量、混乱度、所占体积的函数。
E对S、V、N的偏导则是强度变量。我们定义E对S的偏导就是温度T、对V的偏导是压强p,对N的偏导是化学势μ,这三个量不能相加(强度变量)。它们的作用就是“评价强弱”,对于一般体系而言则可以反应体系的“方向”。
"方向"指什么呢?
高温的A和低温的B接触,发生能量交换,能量自发地从A流向B(热交换),直至温度T相同时达到平衡;高压的A和低压的B进行体积交换,能量自发由A流向B(体积功),直到压力p相同时达到平衡;A和B发生粒子交换,类似T和p,可以定义一个量“化学势”,用来判断粒子交换是否达到平衡和能量变化的“方向”。这就是化学势的意义。
化学势和Gibbs自由能的关系有时怎样的呢?
化学势和活度以及浓度的关系如下,这段物化书上有,就直接截图了,其中+RT ln[ ]大家应该很熟悉了。

对于A和B之间的反应而言:
由上面Gibbs自由能微分式的定义,很容易推出以下的公式。
其中反应进度ξ是用来描述某一化学反应进行程度的物理量,量纲为mol反应,相当于dN。
所以得到了
从以上的推导能看出Gibbs自由能和化学平衡之间的关系。平衡时,Keq=1,ΔG=0,两边化学势相等达到平衡。甚至能估算出ΔG每增加1.36 kcal/mol,平衡常数上升10倍。
当B的Gibbs 自由能比A低时,从A转化到B是放能 的,如果反应开始时A过量,溶液中组分的自发变化过程将朝着生成B的方向进行。相反的,如果B的Gibbs自由能比A高,则该反应是吸能 的,考察Gibbs自由能示意图时我们使用这些名词。 从G = H − T*S中我们知道,自由能包括焓(H) 和熵(S) 两个成分。
ΔG、ΔH单位kcal/mol、ΔS单位 eu=kcal/(mol·K),1 kcal=4.184 kJ
PS.以上推导是从热力学出发的,不涉及到动力学。平衡在时间上可能是无限的长才能达到的。动力学中以上内容有另一番描述,在非平衡热力学中还有“广义热力学力推动下产生广义热力学流”的描述。同一个现象不同视角可以有不同的描述。
焓
焓变是指在恒压不做功的情况下,一个分子集合中两个不同组分之间热量的变化。
PS.这个是有机化学中的简化说法,不是焓的真正定义,很多初学者会有“为什么要定义焓(H:=U+PV),直接用热量Q不好吗”的疑问。这要在物化中才有解释,简单说和“状态函数”相关,H=U+PV是一种勒朗德变换,化学里用的多是因为化学中恒压条件更常见。
焓变和化学键 化学反应中热量的变化通常伴随着两种状态间化学键的变化,这种化学键的变化可以是分子内的也可以是分子间的。因此考察始变的最简单方法就是考察相关的化学键强度的变化。
在本章中将会对化学键强度进行深入探讨。事实上,所有关于张力和稳定性的问题都与化学键强度有关。在本章中将给出几种形式的张力的明确定义,它们包括:角张力、扭曲张力、空间张力 等,每一种张力都是由于分子中化学键的削弱造成的,它们使得分子变得不稳定。
焓的变化一般用“吸热 ”和“放热 ”表示,高中化学知识。
熵
熵是体系混乱度/自由程度的量度。 加热通常导致分子更加元序。化学上描述情最简单的方法是把它与各种类型的分子和原子的运动联系在一起,它们被称为自由度 。熵比温度更本质,这一点很多物化教程都有精彩的表述。
自由度越大,体系越"松弛”,熵就越大。自由度包括三种类型:平动自由度、转动自由度 和振动自由度 。
我们还可以从统计学的角度来研究体系的熵。体系存在越多的构型,对熵就越有利。
这里所说的构型可以粗略地理解为分子的不同的几何形状。分子的可能构象越多就越无序。如果构象的能量都相等,熵随着Rln*n *的增加而增加,这里n表示构象的数目。当不同的构型具有不同的能量时,构型与熵的关系就更加复杂。
基础化学中利用键能将焓和分子结构相联系,熵和分子结构的联系又是如何呢?
一个小分子在浓度为1 mol/ L 的情况下,其平动熵约为30 eu 。溶液浓度越高,分子的运动受到的限制就越多,因此熵就越低。
该数值表明在一个反应中使分子失去平功能力需要30 eu 。一个普通的有机分子其转动熵也大约为30 eu,但它与浓度无关。最后,存在于强共价键中的高频振动对分子的熵没有显著的贡献,但低频振动会对熵有一些贡献。分子内化学键的旋转平均贡献35 eu ,这表明在化学变化中限制一个可自由旋转的化学键需要35 eu。
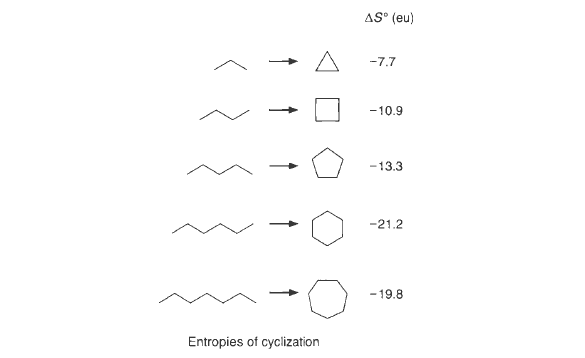
经验上,冻结一根化学键的旋转,平均需要3~5 eu 。
随着环的增大,环化反应的熵变变得越来越不利。(环己烷是一个特例,相对于所有的链状形式,它的熵变是最不利的。)因为当环增大时,需要冻结更多可旋转的化学键才可以成环。
ΔG ΔH ΔS判断化学反应方向时的权重
焓为主、ΔG决定、熵为辅。 这就是高中化学强调焓变的原因。
虽然熵在化学结构发生显著变化(如环化)时非常重要,但是当比较两个相似的结构时,熵变通常很小。由于这个原因,热力学中的讨论主要都集中在焓变上。通常在讨论两个或多个结构的相对稳定性时只考虑焓变的数值就足够了,因为其值在相似的结构中也会有很大的变化。但是必须记住ΔG才是平衡常数的决定因素。只有当焓变的差异非常小时,才需要考虑熵的变化。
2.1.3 键解离能
定义:
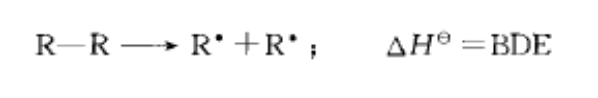
注意是“均裂 ”形成两个自由基,异裂出质子是在酸碱中讨论的。
PS. 在讨论C-F键这种极性很强的键键能的时候,一定要注意键能的定义。一个很经典的问题是:C-F键键能很大,甚至超过C-H键,那为什么氟代的烷烃碱性下也能发生消去反应?
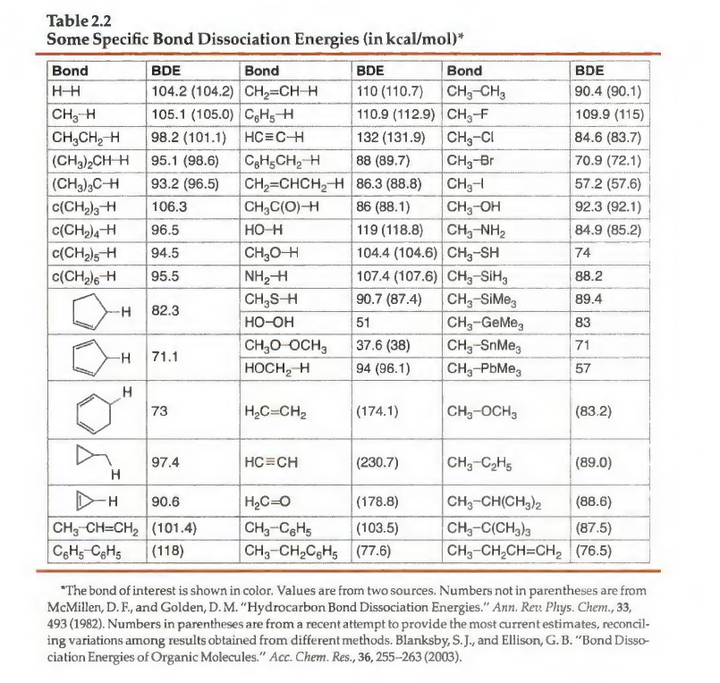
由于BDE可以表示化学键的强度,在一个分子中比较不同化学键的BDE数值就可以知道它们的强弱。对于两个化学键数目和类型都相同的分子,如果假设它们之间熵的差异不是很大,那么通过比较两个分子总的BDE值就可以知道哪一个分子更稳定。
BDE还反映了化学键的本质,所以化学键模型也应该能够解释不同化学键的解离能的不同。
规律和其他热力学数据的类似:
CH3—X中,-F>-OH>-NH2,电负性是主要因素。
结合上一章的内容,我们知道键长越短,键就越强 。
对于卤素而言,是-F>-Cl>-Br>-I。这个不仅和电负性相关,也和键长、轨道重叠相关。
杂化的影响:C(sp)-H>C(sp²)-H>C(sp³)-H。上一章的解释同样适用,s轨道成分越大,基团的电负性就越大,键长就越短。
有机化学中常把饱和碳链看成是惰性的,数据上看C-C和C-H 键的BDE通常都大于85 kcal/ mol 。和其他化学键相比确实非常稳定。相比过氧甲醚的O-O键,BDE 仅为38 kca l/ mol,差距确实非常大 。
再举表里的一个例子:
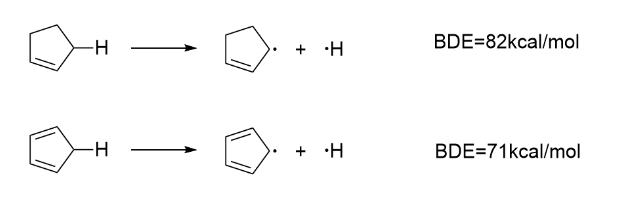
很明显是共轭对自由基的影响,上一章已经讨论过,但这个问题很容易想到芳香性问题上,只能说不要想太多。
水分子中的O-H 键是最强的化学键之一,其BDE 为119 kcal/ mol 。由于在自由基反应中热力学数据往往反映了反应活性,羟基自由基(HO·)具有非常强的反应活性因此也不足为奇。在反应:
HO· + R-H → H2O + R·
中,对于几乎所有的有机化合物RH ,该反应都应该是一个放热反应,并且反应速率很快。
羟基自由基公认是生物系统中最具活性的活性氧物种,它在很多生命物质中都存在并且参与很多生物化学反应,同时有可能能导致生物体内DNA,蛋白质和脂质氧化损伤。
使用BDE 预测反应的放热性和吸热性
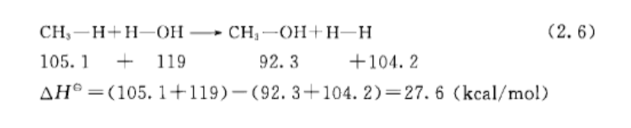
这个在大学化学里应该是基础知识了,就不多说了。注意不同的方法测得的BDE 值会有一些差异,最后不要用不同文献中的数据计算。
2.1.4 势能函数和势能面简介——键伸缩
本节将涉及大量的量子力学内容,没学过的可以只看结论,学过的可以直接跳过。
本段其实想讲的是:熵和键解离能(化合物性质)——键伸缩模型(理论模型)——红外光谱(测试方法),结果花了大功夫讲了一个量子力学模型,不知道意义何在,但我还是摘录了下来,并补了一些概念。
对于一个简单分子,定义BDE 的化学键均裂反应可以与分子的某个简正模式 联系起来。简正模式是分子具有的振动自由度,包括伸缩、弯曲、摇摆、扭曲等,每一项都有它们各自的基频 。分子的结构并不是静态的,而是动态的。每一种基频都可以用一个势能函数 所描述。
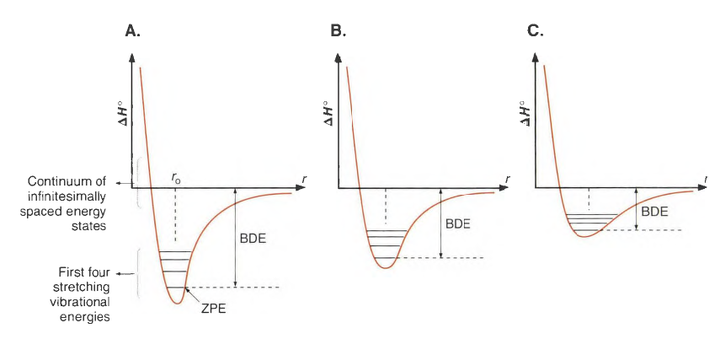
这种图称为Morse,它是一维谐振子的薛定谔方程解的加强版,在物化和谱学原理-红外中都有介绍。它是一种对于双原子分子间势能的简易解析模型。它对Morse势求解Schrödinger方程具有解析解,方便分析问题;另一方面,由于它隐含地包括了键断裂这种现象(横坐标是原子的间距,无穷远即键断裂,最低点即测出的键长,量子化可以理解成是被距离限制在“键长值”附近了 ),对于分子振动的微细结构的具有良好的近似。
Morse势的数学表达如下
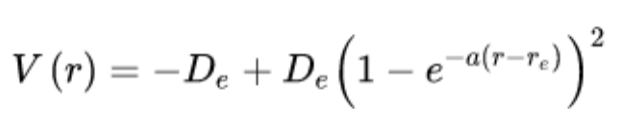
Morse势描述的成键和振动: 由形状可知,当原子间距离很大时,原子相互之间可以自由移动。当原子互相接近到一定距离时,原子轨道发生重叠,使得原子相互吸引,当原子间距离很小时,核的排斥力占主要作用,使得原子被相互排开。图中能量最低的地方表示原子轨道重叠(稳定化)和核间排斥(减稳定化)两种效应达到平衡时的状态。Morse 势能函数的形状表明它是一个非简谐共振子。
最简单的振动能级模型是一维谐振子模型 静态薛定谔方程的解

把最后一个总能量的表达式套入薛定谔方程的哈密顿算符,就有:
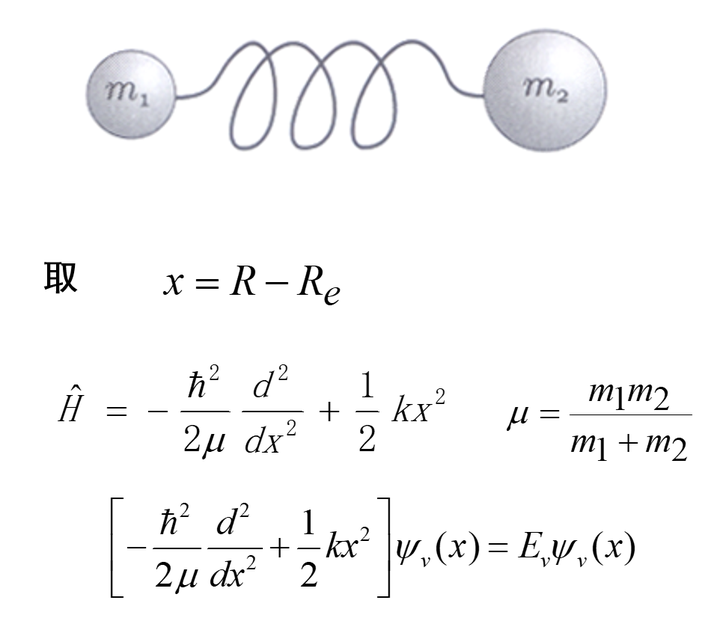
它对应一维谐振子,我们不需要知道怎么解这个方程,只要了解振动态能量和能级的关系是量子化的(能量E和正整数v相关):
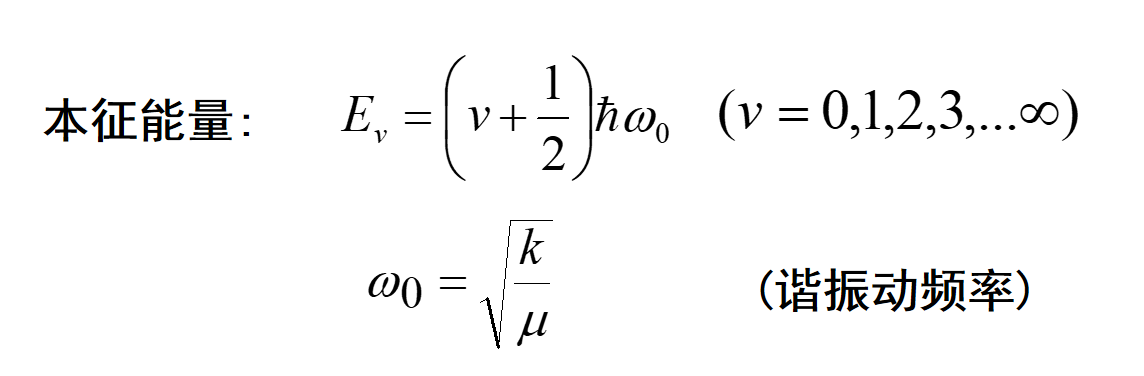
弹簧的力常数k表明键的强度,键越强力常数越大,从而振动频率也越大。从日常生活的经验我们可以知道刚性弹簧振动的基频要大于松弛弹簧振动的基频。化学键在低能振动时具有相同的性质这个公式表面化学键的伸缩振动。
同理,受到Morse 势能函数的限制,振动的能量不是连续的,而是量子化的。依旧可以使用上面的公式,其中中ω表示化学键的角振动频率,每个振动态的能量在Morse势能曲线上以横线表示。能量最低的振动(n=0) 被定义为零点能,这是一个非常重要的概念,讨论同位素效应时会用到它。把下面的公式带到Ev的表达式中就可以计算Ev。
按照键解离能的定义——“使化学键完全解离所需的能量”可知,键解离能就对应势能曲线最低处的零点能(ZPE,注意不是曲线的最低点) 与原子间距离无限大时的参考态能量之间的差值。 这在上面的Morse图中已经标记了出来。
对于一系列量子化的能量状态而言,吸收光子的能量等于两个状态间的能量差,这就是光谱学中红外光谱的基础。
高能振动态的存在也被称为分子的激发振动态。对于大部分有机分子而言,其零点能之上的键伸缩振动态在常温下通常都不会明显存在。(书上这里计算了碳碳单键双键三键的例子) 由于原子的振动,它们的相对位置会随着时间不断变化,这表明键长也随着时间变化。
“在特定距离上发现原子的概率”(这里不知道为什么突然问出只有一个问题)
Morse 势能函数是我们提到的第一个描述特定运动势能面的例子。化学键在Morse 势能函数定义的限制下振动。你也许会问:在某个时刻观察到一个特定的键长的概率是多少?这类似于提问在空间中特定的坐标上发现电子的概率是多少。关于这个问题的答案。
回答很简单——概率正比于波函数模的平方。
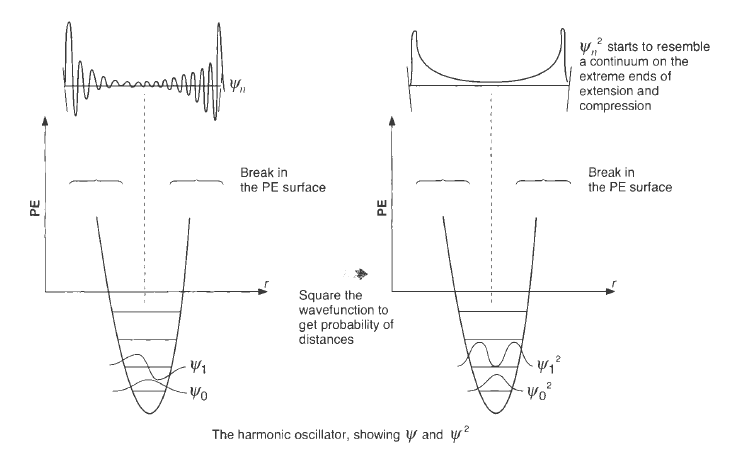
Morse 势能曲线的形状可以表示化学键的强度以及相关振动的松弛程度(即熵)。
前面大篇幅讨论了物化,这里又大篇幅讲起了量子力学,其实这里讲这些内容是为了引出下面这段话:
势阱越深,其键解离能越大,对应化学键就越强。 对于类似的化学键,键越强,振动频率就越高,它表示的势能面就越狭窄(Morse势图A) 。狭窄的势阱对应于刚性振动。当化学键强度减弱时, Morse 势阱变浅,势阱的宽度增大。当振动频率变小时,该振动可以看作是松弛振动(Morse势图B 和C) 。在前面曾经提到刚性振动和松弛振动的概念对于化合物以及化学反应的情很重要。
红外光谱
以上理论的算出来的就是红外的振动峰,其实键角的弯曲、分子的摇摆和剪切振动也都是量子化的,都在红外光谱中可以观测到,但涉及对称性操作,在这里不展开了,只需了解所有的振动自由度都是量子化的(键角可以振动的范围是有限制的) ,每一种运动都可以通过一个势能面来描述它是刚性的还是松弛的,从而可以得出各种振动的熵的相对大小。
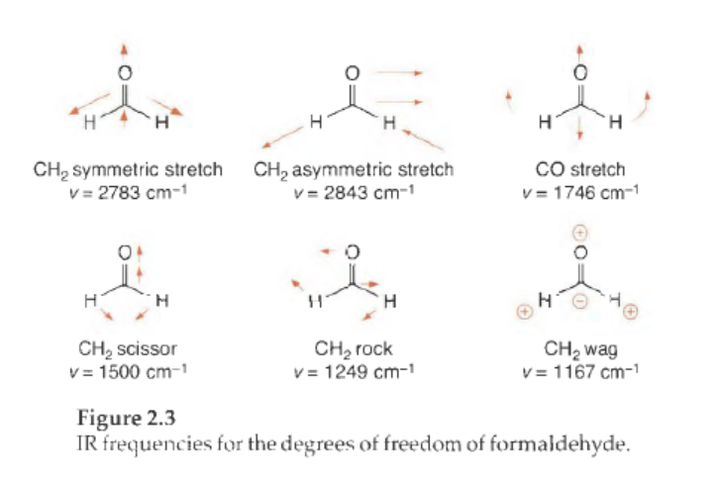
2.1.5 生成热和燃烧热
对于任何一个分子,其总能量 表示断裂分子内所有的化学键,把分子打碎为离散的原子并移除这些原子上所有的电子所需的能量。这个值没什么意义,当然从头算可以算出来。
燃烧热是指物质与氧气进行完全燃烧反应时放出的热量。
生成热是由各种元素的最稳定单质生某纯物质产生的热效应。
要注意“完全燃烧”“最稳定单质”“反应条件”等问题。
碳氢化合物的生成热、燃烧热可以定义如下:
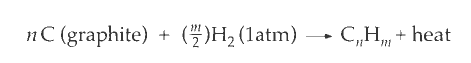
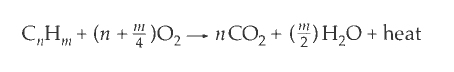
设置燃烧热是因为生成热不好测。
在比较两种或多种同分异构体化合物时,生成热负值越大表明化合物越稳定 。
燃烧热负值越大表明化合物越不稳定,其分子内张力也越大。
由表达式可以知道:
对于A→B
反应焓=A的燃烧焓-B的燃烧焓=B的生成焓-A的生成焓
生成焓可以是正的,热力学不稳定的化合物很常见。
我们必须清楚地了解热力学稳定性和动力学稳定性之间的差别 :
热力学稳定性 与特定的平衡位置相关,它是通过ΔGΘ来衡量的。
动力学稳定性 与反应速率有关,所以控制它的不是ΔGΘ,而是ΔG≠。如果一个分子所有可能发生的反应都存在很高的活化能壁垒,则该分子在动力学上是稳定的。下面这张图是从March里找的,动力学稳定热力学不稳定的例子,比如过氧化氢。
2.1.6 基团加和法
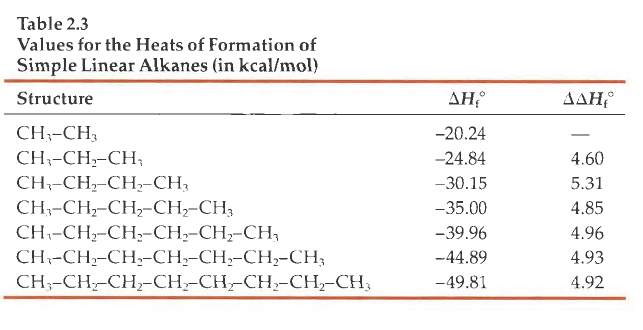
在起初的一些波动之后,规律逐渐显现出来:在正烷烃上每增加一个CH2 基团生成焓平均增加-4.93 kca l/ mol ,该规律暗示了基团加和 的概念。
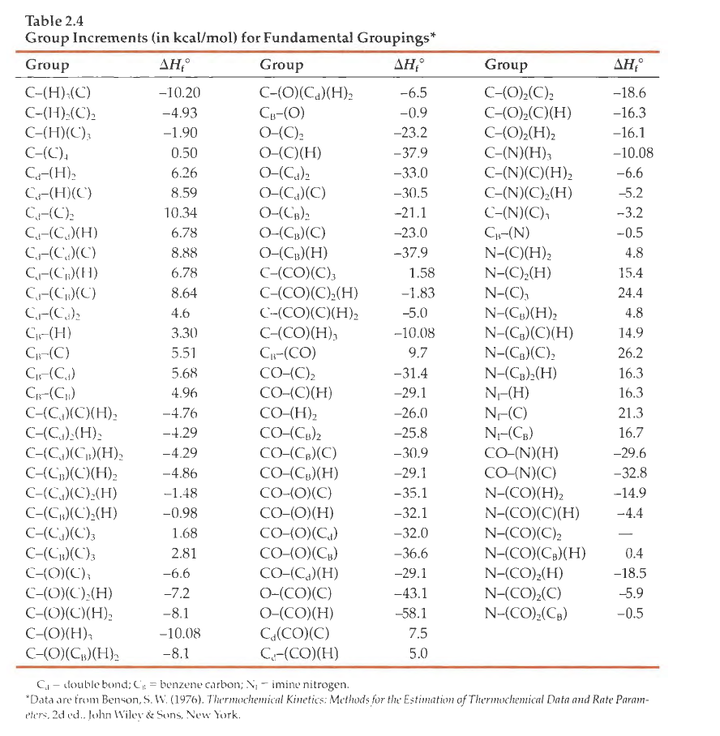
Cd=双键上的碳原子;CB = 苯环上的碳原子;NI= 亚胺上的氮原子。这个表的数据也被称为Benson 增量。
Benson基团加成法对于反应机理的研究, 用来估算分子生成热的可信方法极为重要。
比如,如果算出的一个分子的生成焓超过了一个反应的活化焓与反 应物的生成焓之和,那么,这个分子就不可能是这个反应的中间体。
这个表仔细读会觉得奇怪,因为经计算和验证后发现仅有双原子体系的信息是不够的。很明显并非所有的C-H键都是一样的,于是通过增加基团中原子的数目避免这种情形发生。
所以变成了[某原子]—[相连的原子1]n[相连的原子2]m……这种形式。
这表要细谈可以讲很久,简单介绍的话举个例子:
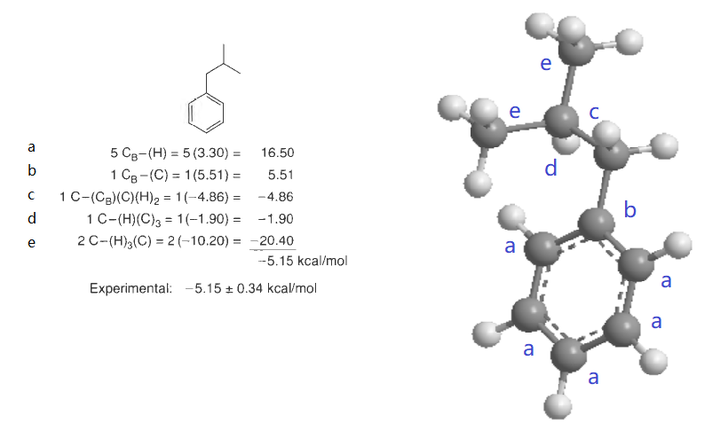
这个例子能看出链接苯环和烷烃的亚甲基C-(CB)(C)(H)2和一般的亚甲基C-(C)2(H)2是不一样的。
该方法的缺点:
使用基团加和法得到的计算结果的准确程度取决于导出基团贡献值的热力学实验数据的准确程度。
一些定义相当含糊的官能团,如偶氮和肟,其基团贡献值也被发表出来。通常包含这类基团的化合物的实验数据很少,所以在使用这些基因贡献值的时候应该特别小心。
基团加和法忽略了基团间的相互作用,这些作用有时候对生成热也有不可忽视的贡献。这里有一些基团加和法失败的例子,其失败的原因不是由于缺乏足够的热力学实验数据,而是因为对基团之间的相互作用考虑不周。
另外要提的参数,比如“生成熵”,它也可以用上面的方法做出“基团加和法表”,但它讨论少的原因是可现有的可参考的数据太少了;还有热容Cp,它可以反应焓变随稳定的变化,化工行业中也很常用。
2.1.7 张力能
既然使用化合物的标准生成热来明确定义化合物的稳定性,现在就可以讨论张力这个概念。在本章的开头引入了张力的概念。这就是为什么本段说了那么多有的没的。
张力是由于分子内的化学键、结构或构象的扭曲而产生的内部应力。 如果有办法预测一个不存在任何键扭曲的分子的稳定性,也就可以为张力能给出一个精确定义。
基团加和法可以被用来计算有机分子的标准生成热,在此方面它的确是一个很强大的工具。

上图中的偏差来自于小的环系是存在张力的。环戊烷分子在某种程度上存在张力,环丁烷和环丙烷分子内的张力就更大一些。这种张力部分来源于环上的C-C-C键角相对于标准的C-C-C键角发生的明显扭曲。(其实Benson及其合作者已经把这一研究进一步扩展到包括杂原子和不饱和的化合物有关基团的贡献值及环状化合物的修正值。)
基团加和法当然没有考虑环内的张力。因为这种方法在参数化的时候仅仅考虑一些简单的、不存在成键扭曲的非环烷烃,所以它不适用于环烷烃。
我们网此可以明确定义张力能的概念——张力能 就是一个分子由实验测定的标准生成热与用基团加和法预测的标准生成热之间的差值。
我们可以尝试着把张力能分解为键角张力、二面角张力和环张力等,将在本章中对此进行讨论。这种做法从原则上讲是非常危险的。因为如果用量子力学来描述化学键,将不能自然而然地导出以上这种对张力能的划分方案。所以必须进行人为的划分。事实上这也是很有用的策略,但是我们在应用它的时候一定要谨慎。
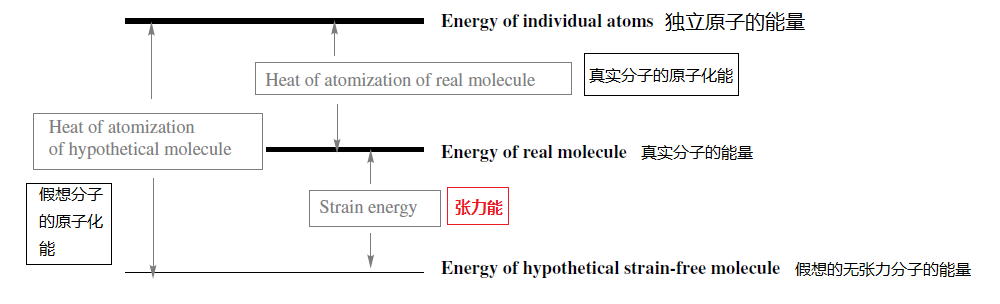
March里的这张图比较直观,所以贴过来了,但注意不同的书张力能定义不一样,March的图只是给了一个笼统的说法。